@greweb - Bezier Curve based easing functions – from concept to implementation

EDIT 2014: This article ends up in an updated library available on NPM (bezier-easing) and available on Github. It has been used by Apple for the mac-pro page and by Velocity.js. You can also find its usage in the glsl-transition examples.

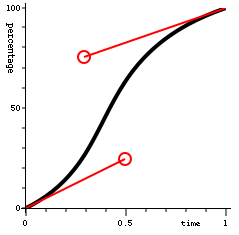
Many animation libraries are today using easing functions – functions of time returning a progression percentage value. This is required to perform such cool effects:

But most of these libraries implement a huge collection of functions. We will see how we can generalize them with bezier curves.

For instance, we use to do this:

EasingFunctions = {
  linear: function (t) {
    return t;
  },
  easeInQuad: function (t) {
    return t * t;
  },
  easeOutQuad: function (t) {
    return t * (2 - t);
  },
  easeInOutQuad: function (t) {
    return t < 0.5 ? 2 * t * t : -1 + (4 - 2 * t) * t;
  },
  easeInCubic: function (t) {
    return t * t * t;
  },
  easeOutCubic: function (t) {
    return --t * t * t + 1;
  },
  easeInOutCubic: function (t) {
    return t < 0.5 ? 4 * t * t * t : (t - 1) * (2 * t - 2) * (2 * t - 2) + 1;
  },
  easeInQuart: function (t) {
    return t * t * t * t;
  },
  easeOutQuart: function (t) {
    return 1 - --t * t * t * t;
  },
  easeInOutQuart: function (t) {
    return t < 0.5 ? 8 * t * t * t * t : 1 - 8 * --t * t * t * t;
  },
  easeInQuint: function (t) {
    return t * t * t * t * t;
  },
  easeOutQuint: function (t) {
    return 1 + --t * t * t * t * t;
  },
  easeInOutQuint: function (t) {
    return t < 0.5 ? 16 * t * t * t * t * t : 1 + 16 * --t * t * t * t * t;
  },
};

Defining such functions is lot of math fun but it is very specific and not really customizable. Hopefully, we can generalize these easing functions. With Bezier curves.

In fact, this work has already been done in CSS Transitions and CSS Animations specifications! You can use transition-timing-function CSS property and give a cubic-bezier(x1, y1, x2, y2) value (all ease, linear, ease-in, ease-out, ease-in-out values are just fallbacking on this cubic-bezier usage).

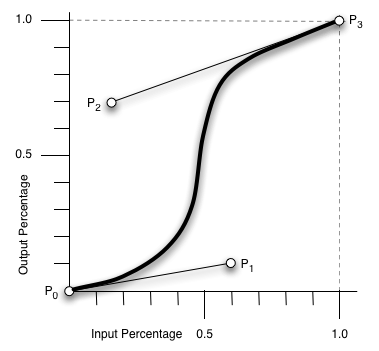
In a bezier curve based easing function, the X axis is the time axis whereas the Y axis represents the percentage of progress of the animation.
The two points P1 and P2 are called handles and you can (exclusively) control their X and Y positions to generate every possible cubic timing function.

Live demo

Try to interact with the handles:

Implementation

Ok, so, this bezier curve concept is great but how can I implement it?

I’ve read here how simple is it to compute many points of a Bezier curve and potentially draw them:

function B1(t) {
  return t * t * t;
}
function B2(t) {
  return 3 * t * t * (1 - t);
}
function B3(t) {
  return 3 * t * (1 - t) * (1 - t);
}
function B4(t) {
  return (1 - t) * (1 - t) * (1 - t);
}
function getBezier(percent, C1, C2, C3, C4) {
  var pos = new coord();
  pos.x =
    C1.x * B1(percent) +
    C2.x * B2(percent) +
    C3.x * B3(percent) +
    C4.x * B4(percent);
  pos.y =
    C1.y * B1(percent) +
    C2.y * B2(percent) +
    C3.y * B3(percent) +
    C4.y * B4(percent);
  return pos;
}

But it’s not enough. We need to project a point to the Bezier curve, in other words, we need to get the Y of a given X in the bezier curve, and we can’t just get it with the percent parameter of the Bezier computation.
We need an interpolation.

Deep into Firefox implementation

In Mozilla Firefox, The bezier curve interpolation is implemented in nsSMILKeySpline.cpp : .

What we can learn from it is:

A first optimization store sample values of the bezier curve in a small table used to roughly find a initial X guess.
Then, it use two different implementation strategies: One use the Newton’s method and the other is just a dichotomic search (binary subdivision).
A criteria based on the slope give the best strategy to take.

These sub-optimizations probably make the difference for the C++ version but are not really relevant for the JavaScript implementation. Moreover, I have only used the Newton’s method algorithm.
And this is the code:

Now we can just alias some classic easing function – like CSS does.

I’m working on the next version of Slider.JS which relies on 3 different technologies for image transitions: CSS Transitions, Canvas and GLSL shaders (from WebGL).

I have now found a common way to describe easing functions for both CSS-based and Javascript-based animations!

This example has shown that sometimes, finding a larger solution for a problem is more interesting than having specific solutions.
This is called the Inventor’s paradox.