Every NFT sold allows acquiring a plotted frame. (code in the unlockable content)
My 7th plotloop is a very special one, inspired from the mother of all of my plot loops: plot#108 which wasn't planned to be animated but a way to visualize randomness and chose one frame! This is still what gave me the idea to do these plot loops.
The concept of Plot Loop, as described in https://greweb.me/2021/05/plot-loops article, is an hybrid concept between a digital video art and physical plot that produces topology of the same art.
The main digital art is a 1920p video loop of 8 frames available as NFT on Opensea.io sold by @achetezdelart famous Paris' art gallery. I am so thrilled to work for the first time with an art gallery and looking forward to do more collaboration in the future! The physical art is the 8 frames, plotted with 3 fountain pens on Bristol A4 paper (250g), and offered when buying the NFT.
24+ hours of near non-stop plotting!
Once the coding was done, the hard part was the precision work of plotting 8 frames, each taking 2 hours to achieve. With all the fail and retry there were, it took me more than a day to finish it all. The sun strokes takes about 10 minutes but the rest takes around 100 minutes.
Zoom photos

"Proof of Plot", a very time-consuming creation process
The creation process of this plot loop was one of the most challenging one, among all of the other plots I have done so far. The fact each frame takes about 2 hours to plot with 2 manual actions (changing the fountain pens) makes any mistake very punishing! You can't faster the 2 hours much without risking the paper to suffer faced to the number of stroke of the fountain pen!
Fail and retry
Yet, plotting is a fail and retry process, so I like to show you 2 failures first among 4 of my first prototype fails:


For anyone familiar with plot and fountain pens this is indeed one of the worse nightmare to deal with: too much stroke-crowded area is going to badly end up with literally digging through the paper.
Quick technique to solve this problem
A very simple technique I call the "passage counter" technique. It's simply the use of a 2D Grid where each cell have a counter that you increment when a line goes through it, when it reaches 3 (or more) that's where you start raising the pen in these crowded area.
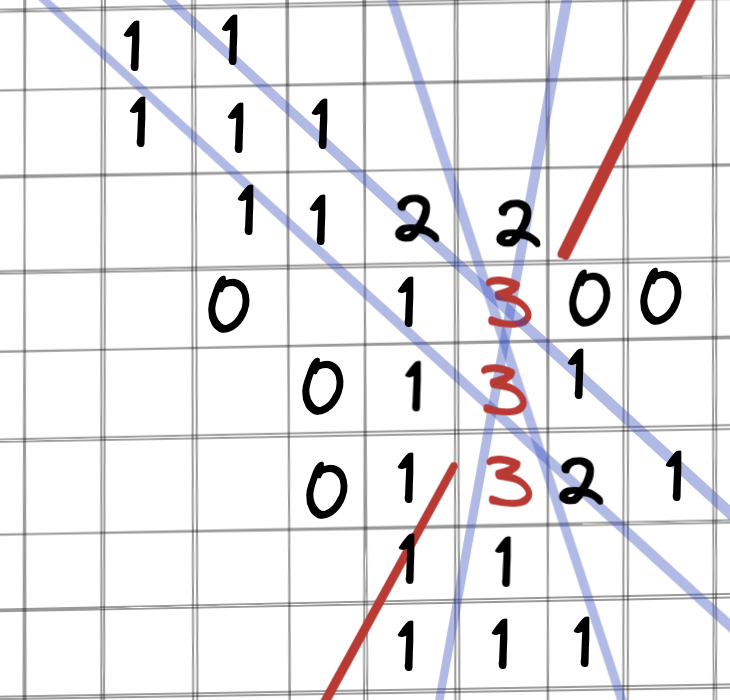
It works great with the limitation that too much up and down of your pen is both time consuming but also can be hurting the paper too, there there is a tradeoff to find.
Some interesting creative coding techniques used
sun rays projection
For the sun rays, I've used a simple radial projection that collides with the mountain lines.
I had to make lines randomly starting at different places to avoid the effect to be too condensed at the beginning (problem of radial projection is your lines get more and more distanced). I wanted it to not be that "random" so i've used a simple prime number formula: distance to center of sun is added of an extra 8. + ((i * 29) % 121) as f64 where i is the ray index.
sun oscillation
I didn't wanted to make the sun motion too realistic but I wanted a visible motion that would fit with the mountains and project rays from different positions. It also had to be looping (which a sunset/sunrise wouldn't allow)
Therefore, I went with a simple trigonometry formula:
let sunp = (
w / 2. + 75. * (2. * PI * sunphase).cos(),
50. - 30. * (2. * PI * sunphase).sin().abs()
);
mountain oscillation and noise shape
The noise algorithm I used was much more accomplished than in plot#108 even though that historical plot one is interesting too.
I learned recently the power of 'domain warping' on applied on noise and I applied it here, at least mainly on the 1D of the wave. It creates more "local minima" on the shape and creates a more interesting animation.
It's important to also note that noise/perlin noise, is quite challenging to "loop" and the way I did this is interpolation between 3 states. I have simply done this:
let n1 = perlin.get([ a, b, opts.seed + i as f64 * divergence + 200.2 ]);
let n2 = perlin.get([ a, b, opts.seed + i as f64 * divergence + 300.514 ]);
let n3 = perlin.get([ a, b, opts.seed + i as f64 * divergence + 400.31 ]);
let n = 0.8 *
(
n1 * (2. * PI * p).cos() +
n2 * (2. * PI * (p + 0.33)).cos() +
n3 * (2. * PI * (p + 0.66)).cos()
) +
// global disp
0.2 * perlin.get([
freq * xp,
freq * y,
opts.seed
]);
where a and b are noise themselves to apply the "domain warping" magic.
