Here is "Dancing Planet", my 5th plot loop (see article). The main digital art is a 1920p video loop of 8 frames available as a Tezos hicetnunc NFT. The physical art are the 8 frames, plotted with 2 fountain pens on Bristol A4 paper (250g), and offered when buying the NFT.
There are 8 plots available for sale and there will be no other editions of these plot loop frames. They all have the same inital price and the physical piece is selected in order of buy as each frame is relatively similar!
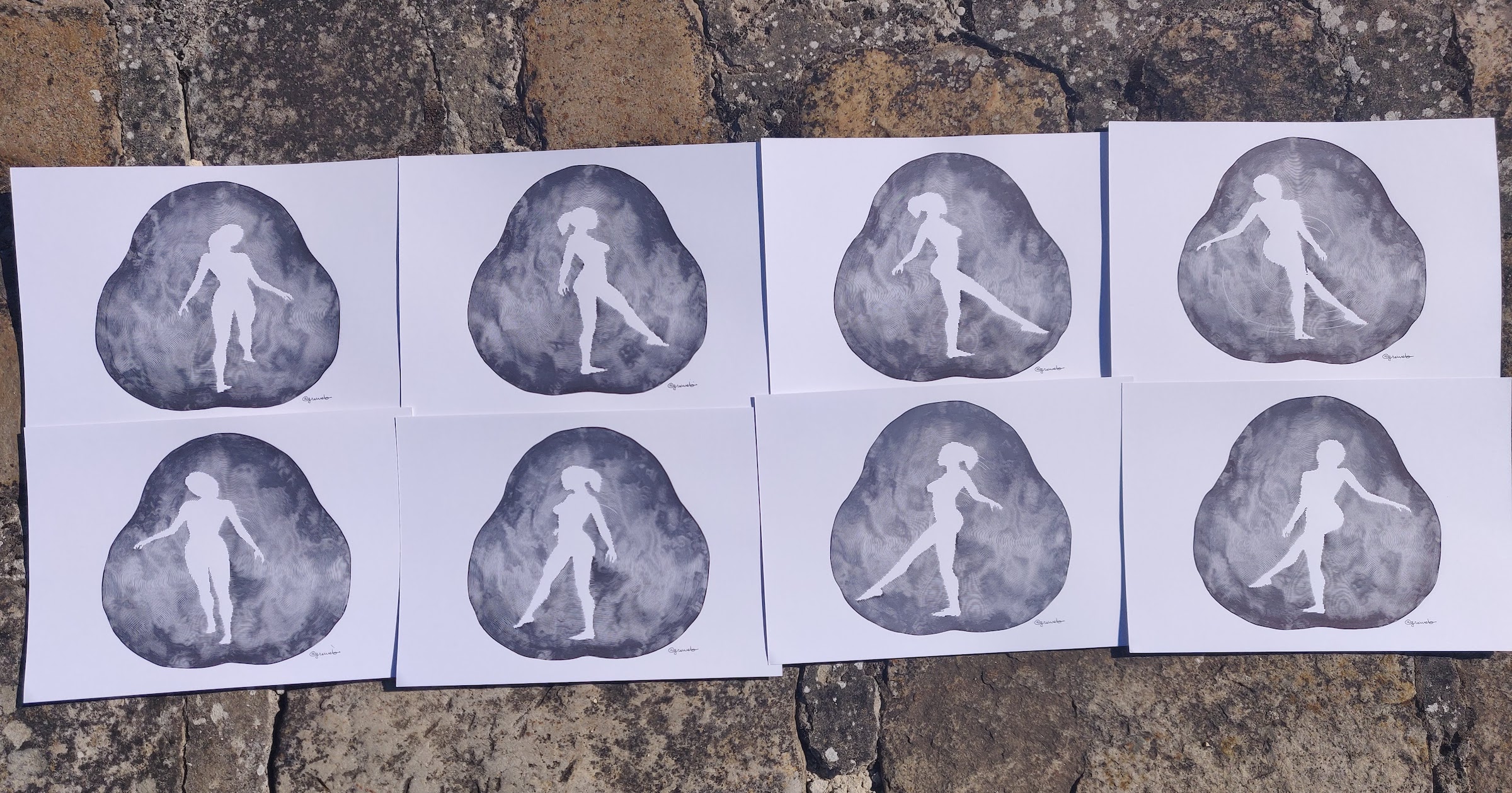
This is a reboot of plot#148 but with a big rework of the noise technique using domain warping as well as combination with this famous 'rotating dancer' GIF.
It is plotted with two phases, a first pass without a lot of noise and a second pass with more noise divergence:



Early prototype, in pursuit of the good ink and paper...
I started with this first prototype of the concept:

It allowed me to see what I could adjust, for instance: adding more noise, more lines and scaling a bit the dancer.
I used ink 'Quink' by Parker plotted with a fountain pen on a Canson Bristol 250g paper (A4 format).
Here is another prototype I tried: it uses a mix of two colors (dragon red and turquoise). I ended up preferring minimalism: black on white. At the end I stayed on my first ink choice but I will revisit this idea.


Process to find the final plot
To search for the good parameters I've used a generator script with bash for loops. It kinda looked like this:
for a in 0.5 1 2 4; do
for b in 0.5 1 2 4; do
for c in 0.5 1 2 4; do
for d in 0.5 1 2 4; do
sh $P/gen.sh --a $a --b $b --c $c --d $d
cp ./results/out.gif out/${a}_${b}_${c}_${d}.gif
done
done
done
done
Then I kept refining my "range" by fail and retry. It is quite slow to generate them so it's a long process.
When I was satisfied by the parameters, I then switch to a second selection: the selection of the seed! because my noise have seed and can generate very different kind of noises, I put it against my "elector" homemade tool as explained on plot#143.
Some highlight of the Rustlang code
There is nothing really "new" from my previous plots, especially all the parametric plot when I started this "growing parametric" exploration between plot#114 and plot#148.
What is new here however is the use of a GIF as an input. It's very easy to do: my script takes basically an loop percentage which I can transpose to looking up a frame in the rotating dancer loop. I can then use this function I've just added to my utilities:
use image::AnimationDecoder;
use image::RgbaImage;
use image::gif::GifDecoder;
use image::io::Reader as ImageReader;
pub fn image_gif_get_color(
path: &str,
index: usize
) -> Result<
impl Fn((f64, f64)) -> (f64, f64, f64),
image::ImageError,
> {
let file_in = File::open(path)?;
let decoder = GifDecoder::new(file_in).unwrap();
let frames = decoder.into_frames();
let frames = frames.collect_frames()?;
let img = frames.get(index % frames.len()).unwrap();
let buffer = img.buffer();
return Ok(dynamic_image_get_color(buffer.clone()));
}
pub fn dynamic_image_get_color(
img: RgbaImage
) -> impl Fn((f64, f64)) -> (f64, f64, f64) {
let (width, height) = img.dimensions();
return move |(x, y): (f64, f64)| {
let xi = (x.max(0.0).min(1.0)
* ((width - 1) as f64)) as u32;
let yi = (y.max(0.0).min(1.0)
* ((height - 1) as f64))
as u32;
let pixel = img.get_pixel(xi, yi);
let r = (pixel[0] as f64) / 255.0;
let g = (pixel[1] as f64) / 255.0;
let b = (pixel[2] as f64) / 255.0;
return (r, g, b);
};
}
Rust really shines in having great library, this is just the classical "image" package here.
Apart from this, the Rust code (you can see main.rs link on top of this page) is pretty straightforward. There is just a lot of work in the parametric function which starts to be quite big:
let parametric = |p: f64| {
let p1 = (splits * p).floor();
let p2 = splits * p - p1;
let t = (p1 + split_threshold * p2) / splits;
let mut t2 = (p1
+ split_threshold * p2.powf(pow))
/ splits;
let initial = 1. / spins;
t2 =
(t2 - initial).max(0.) / (1. - initial);
let scale = 1.0
- t2 * (1.0
- i as f64 * opts.size_diff / size);
let s = spins;
let mut p = (
scale
* amp1
* ((s * 2. * PI * t).sin()
+ amp2
* mix(
(s * f1.1 * PI * t).sin(),
(s * f2.1 * PI * t).sin(),
t,
)),
0.07
- scale
* amp1
* ((s * 2. * PI * t).cos()
+ amp2
* mix(
(s * f1.0 * PI * t).cos(),
(s * f2.0 * PI * t).cos(),
t,
)),
);
let noise_angle = p.1.atan2(p.0);
let noise_amp = 0.003 * perlin.get([
opts.a * (progress * PI).sin() +
4.8 * p.0 + perlin.get([
7.8 * p.0,
4.2 * p.1 + opts.b * (progress * PI).sin(),
40. + opts.seed
]),
4.8 * p.1 + 0.8 * perlin.get([
4.5 * p.0 + opts.c * ((1. - progress) * PI).sin(),
6.8 * p.1 + perlin.get([
20.5 * p.0 + opts.d * (2. * PI * progress).cos(),
20.8 * p.1,
200. + opts.seed,
]),
20. + opts.seed,
]),
100. + opts.seed + i as f64 * opts.seed_diff,
]) +
0.03 * (1. - t) * perlin.get([
0.7 * p.0 + perlin.get([
2.9 * p.0 + opts.e * (2. * PI * progress).cos(),
1.7 * p.1,
2000.0
]),
0.7 * p.1 + perlin.get([
3.1 * p.0,
2.5 * p.1 + opts.e * (2. * PI * progress).sin(),
2100.0
]),
1000.,
]);
p.0 += noise_amp * noise_angle.cos();
p.1 += noise_amp * noise_angle.sin();
p
};
